A Real Capacitor
CHAPTER 44.4 A Real Capacitor A real capacitor modeled only as a capacitor, does not exist. All capacitors have finite lead length, and some parasitic which makes a real capacitor a series combination of a resistor, an inductor and a capacitor. The equivalent circuit of a real capacitor is therefore given by
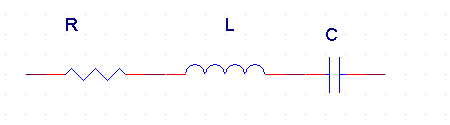
Figure 4 4 - A real capacitor The equivalent impedance of a real capacitor is therefore given by
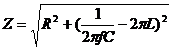
where,
C = Capacitance of the capacitor
L = Parasitic inductance of the capacitor
R = Parasitic resistance of the capacitor
f = frequency
A very important application of this equation is in the area of decoupling capacitor used in power supply. We can no more say that a capacitor provides a “short” at higher frequencies. We can see that at some very high frequency f, the term 2 f L becomes very high as compared to the term . The impedance offered by the lead inductance of the capacitor, therefore, becomes high, so much so that the low impedance path created by the capacitor impedance term becomes ineffective beyond some high frequency f.
It is therefore necessary to choose a decoupling capacitor with as small parasitic inductance as possible. The mounting inductance of a capacitor plays an important role in overall inductance calculation. The mounting inductance will depend upon the trace and the via connecting the capacitor to the power and ground planes. A typical 0603, 0.1uF ceramic capacitor has and effective series inductance of 0.7 nH.
Previous - Capacitor Impedance Next - Capacitance Per Unit Length